Определение точки

Что такое точка? Определение точки в математике и геометрии. Различные понятия точки и их свойства. Геометрические объекты, состоящие из точек. Обозначение точек и линий. Различные виды линий. Заключение о роли точки в математике и геометрии.

Определение точки

Точка является одним из фундаментальных математических объектов, свойства которого задаются системой аксиом. В геометрии, математическом анализе и других разделах математики точку можно представлять как неделимый элемент соответствующего математического пространства. В классической геометрии и большинстве её обобщений все геометрические фигуры, такие как прямые, кривые и тела, считаются состоящими из точек.

Различные понятия точки

Понятие точки может немного отличаться в разных разделах математики. В пространствах с системой координат точка задаётся набором своих координат и обычно отождествляется с ним. Однако понятие точки также используется в пространствах без системы координат, например, в топологии или в теории графов.

Свойства точек

Геометрические точки не имеют измеримых характеристик, таких как длина, площадь или объём, за исключением их координат. Однако в конкретных областях математики некоторые виды точек могут иметь специальные свойства и названия, такие как особые точки, предельные точки и критические точки. В физике также вводится понятие материальной точки, которой приписывается определённое значение массы и динамических характеристик, таких как скорость и ускорение.

Точка в евклидовой геометрии

В евклидовой геометрии точка является первичным понятием, задаваемым перечнем своих свойств - аксиом. В выбранной системе координат любую точку двумерного евклидова пространства можно представить как упорядоченную пару действительных чисел (x; y), а точку n-мерного евклидова пространства можно представить как кортеж из n чисел (a1, a2, ..., an).

Геометрические объекты, состоящие из точек

Многие объекты в евклидовой геометрии состоят из бесконечного набора точек, которые соответствуют определённым аксиомам. Например, прямая представляет собой бесконечное множество точек, а плоскость - бесконечное множество прямых. Отрезок является частью прямой, ограниченной двумя точками, и имеет конкретную длину, которая является наикратчайшим расстоянием между этими двумя точками.

Обозначение точек и линий

Точки обозначаются цифрами или заглавными (большими) латинскими буквами. Несколько точек различаются разными цифрами или буквами, чтобы их можно было различать. Линии, которые состоят из множества точек, обозначаются строчными (маленькими) латинскими буквами.

Примеры обозначений:

• Точки: точка A, точка B, точка C;
• Точки: точка 1, точка 2, точка 3;
• Линии: линия a, линия b, линия c.

Различные виды линий

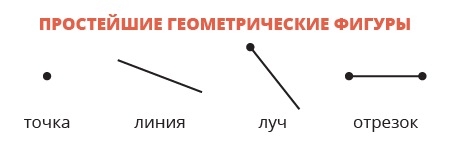
Линия может быть прямой, лучом, отрезком или ломанной линией.

Прямая линия

Прямая линия - это линия, которая не искривляется и не имеет ни начала, ни конца. Её можно бесконечно продолжать в обе стороны. Прямую линию обозначают строчной (маленькой) латинской буквой или двумя заглавными (большими) латинскими буквами - точками, лежащими на прямой.

Луч

Луч - это часть прямой, которая имеет начало, но не имеет конца. Её можно бесконечно продолжать только в одну сторону. Луч обозначается строчной (маленькой) латинской буквой или двумя заглавными (большими) латинскими буквами, где первая - это точка, с которой начинается луч, а вторая - точка, лежащая на луче.

Отрезок

Отрезок - это часть прямой, которая ограничена двумя точками и имеет начало и конец. Отрезок обозначается двумя заглавными (большими) латинскими буквами, где первая - это точка, с которой начинается отрезок, а вторая - точка, которой заканчивается отрезок.

Ломанная линия

Ломанная линия - это линия, состоящая из участков прямых линий, соединяющих последовательные точки. Ломанная линия обозначается строчной (маленькой) латинской буквой или несколькими заглавными (большими) латинскими буквами, где каждая буква соответствует точке на ломаной линии.

Заключение

Точка является одним из основных понятий в математике и геометрии. Она представляет собой неделимый элемент математического пространства и используется для определения других геометрических объектов. В разных разделах математики понятие точки может иметь некоторые отличия, но в целом оно остаётся одним из фундаментальных и неопределяемых объектов.

Что нам скажет Википедия?

То́чка — один из фундаментальных (неопределяемых) математических объектов, свойства которого задаются системой аксиом. Нестрого можно представлять точку как неделимый элемент соответствующего математического пространства, определяемого в геометрии, математическом анализе и других разделах математики. В классической геометрии и в большинстве её обобщений все геометрические фигуры (прямые, кривые, тела и т. д.) считаются состоящими из точек.

При этом в разных разделах математики понятия точки могут отличаться. В пространствах с системой координат точка задаётся набором своих координат и обычно отождествляется с ним. Однако понятие точки используется и в пространствах без системы координат (например, в топологии или в теории графов).

Геометрические точки, вообще говоря, не имеют никаких измеримых характеристик (длины, площади, объёма и т. д.), кроме координат. В конкретных областях математики отдельные виды могут иметь специальные свойства и названия — например, особые точки, предельные точки, критические точки и т. п. В физике вводится понятие материальной точки, которой приписывается определённое значение массы и динамических характеристик (скорость, ускорение и т. д.).

Точка в евклидовой геометрии

Евклид первой аксиомой в своих «Началах» определил точку как «объект, не имеющий частей». В современной аксиоматике евклидовой геометрии точка является первичным понятием, задаваемым лишь перечнем его свойств — аксиомами.

В выбранной системе координат любую точку двумерного евклидова пространства можно представить как упорядоченную пару (x; y) действительных чисел. Аналогично, точку n-мерного евклидова пространства (а также векторного или аффинного пространства) можно представить как кортеж (a1, a2, … , an) из n чисел.

Многие объекты в евклидовой геометрии состоят из бесконечного набора точек, которые соответствуют определённым аксиомам. Например, прямая — это бесконечное множество точек вида L = {(a1, a2, ...an)|a1c1 + a2c2 + ...an cn = d}, где c1...cn и d — константы, а n — размерность пространства. Существуют аналогичные конструкции, которые определяют плоскость, отрезок и другие связанные понятия. Сегмент прямой, состоящий только из одной точки, называется вырожденным отрезком.

В дополнение к определению точек и объектов, связанных с точками, Евклид также постулировал ключевую идею, что любые две точки могут быть соединены прямой линией. Это позволило построить почти все геометрические понятия, известные в то время. Однако постулат Евклида о точках не был ни полным, ни окончательным, и содержал также положения, которые не следовали непосредственно из его аксиом, такие как упорядочение точек на прямой или существование определённых точек. Современные расширения системы Евклида устраняют эти недостатки.