Зачем нужен отчет P&L

Отчет о прибылях и убытках (P&L) является важным инструментом финансового анализа компании. Он предоставляет информацию о том, сколько компания зарабатывает и теряет, а также помогает определить ее прибыльность. Узнайте, как отчет P&L строится, из чего он состоит и как его применять для управления бизнесом. ПингвинКапитал.

Зачем нужен отчет P&L

Отчет о прибылях и убытках (P&L), также известный как отчет о доходах и расходах или отчет о прибылях и убытках, является важным инструментом финансового анализа компании. Он предоставляет информацию о том, сколько компания зарабатывает и теряет, а также помогает определить ее прибыльность.

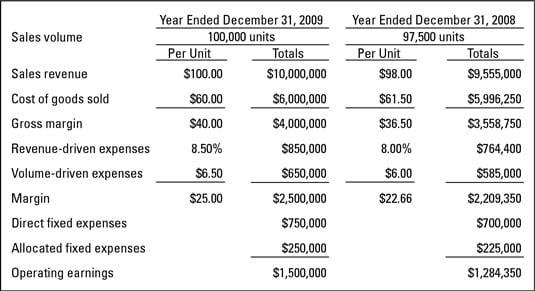
Отчет P&L показывает общую выручку компании, а также все операционные расходы, такие как аренда офиса, налоги, логистика, зарплата, закупка расходных материалов и другие расходы, связанные с основной деятельностью компании. Он также включает операционную прибыль, которая является ключевым показателем, на который следует обратить внимание при анализе отчета P&L.

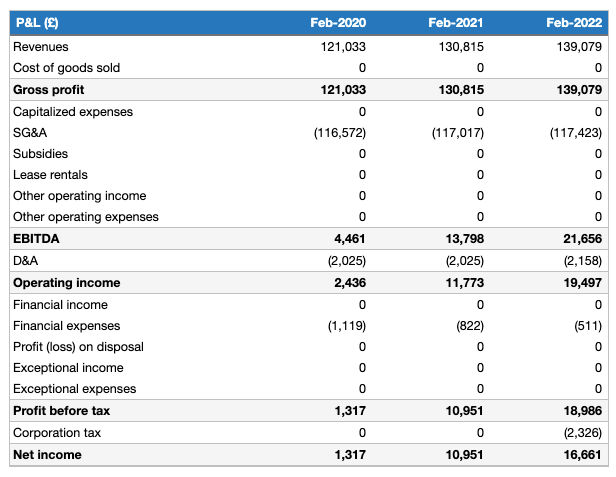
Из чего состоит отчет P&L

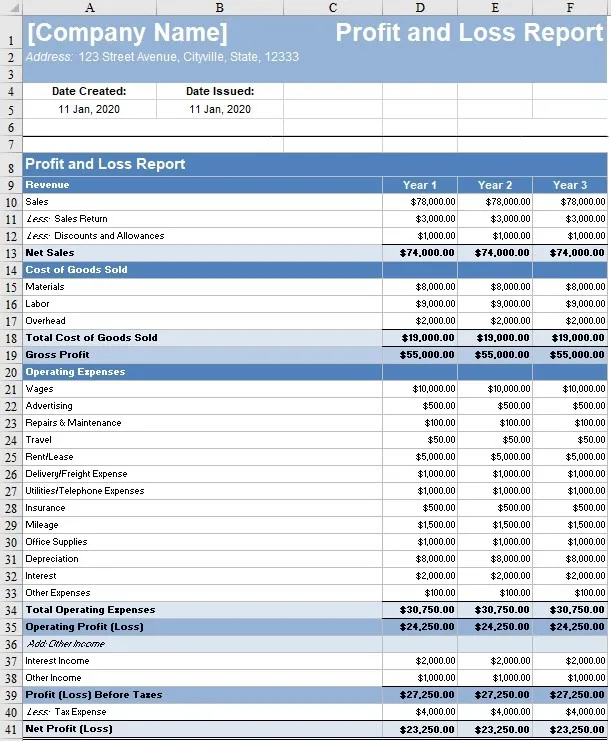
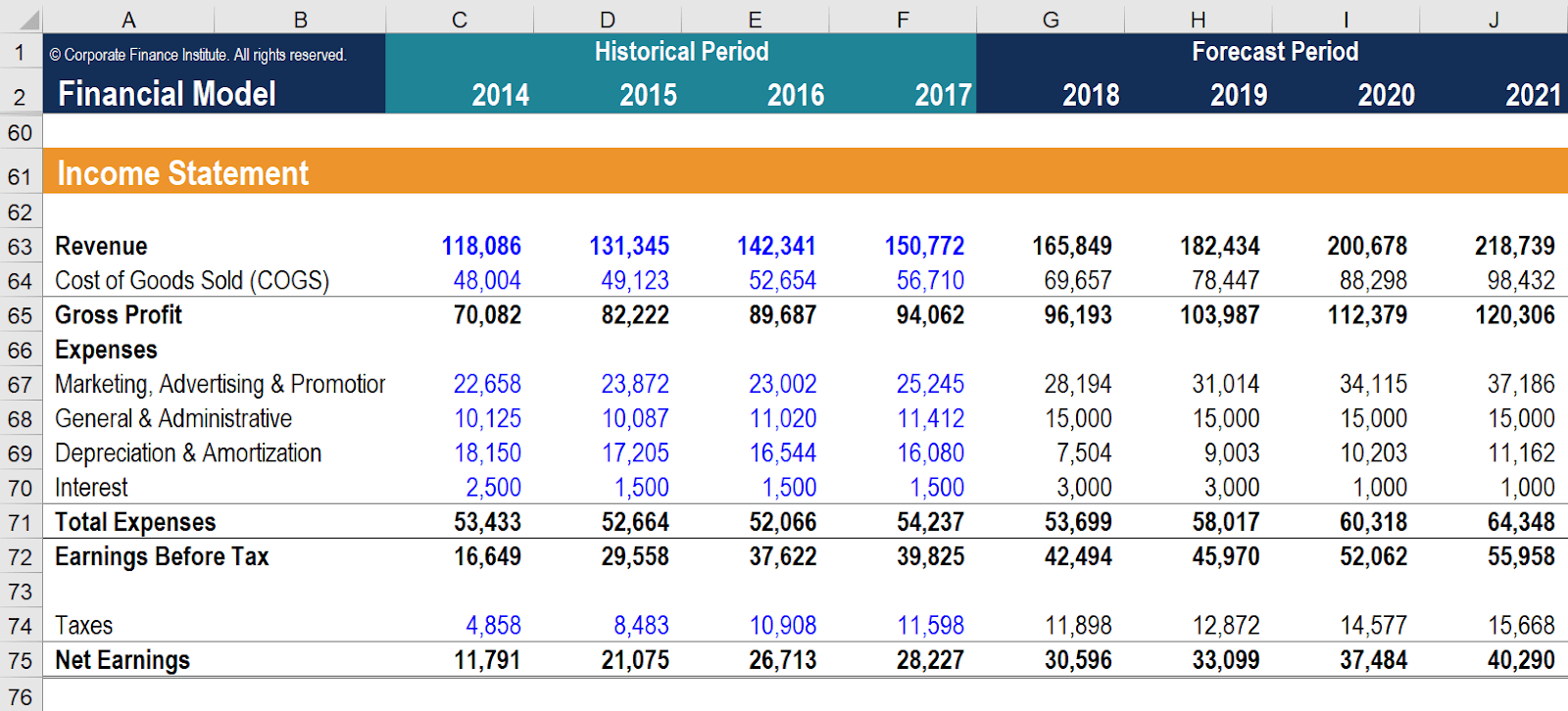
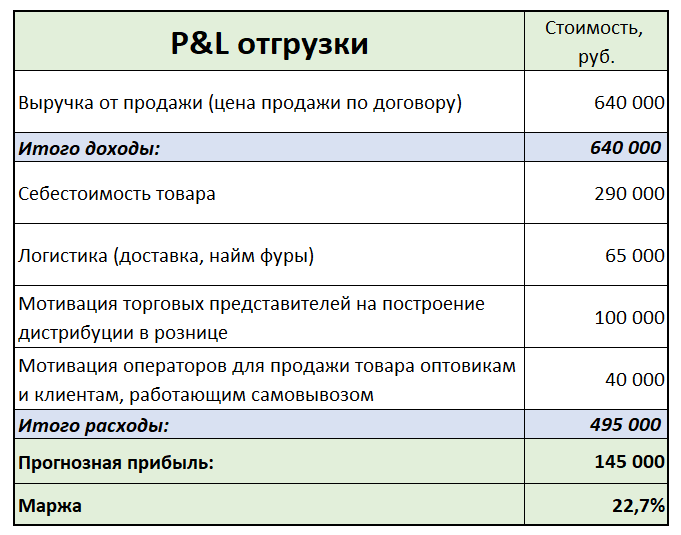
Отчет P&L состоит из нескольких частей:

1. Выручка - общая сумма денег, полученных компанией от продажи товаров или услуг.
2. Расходы - все операционные расходы, связанные с основной деятельностью компании, такие как аренда офиса, зарплата, налоги и другие расходы.
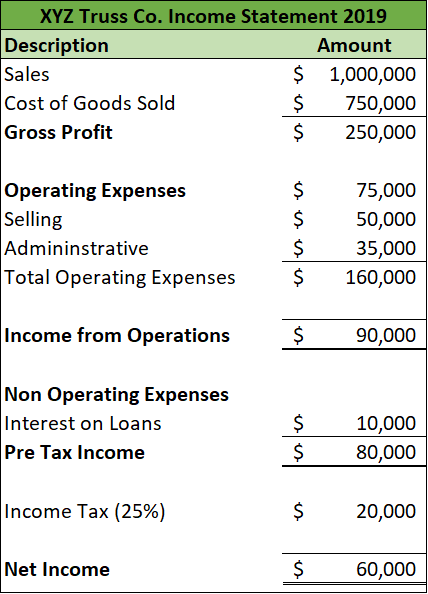
3. Операционная прибыль - разница между выручкой и операционными расходами. Она показывает, сколько прибыли компания получает от своей основной деятельности.
4. Рентабельность - это процент операционной прибыли от выручки. Она позволяет оценить эффективность работы компании.

Построение отчета P&L

Отчет P&L строится по дате начисления. Например, зарплата за апрель будет отображаться в расходах за май. Исключение составляют операции, привязанные к заказу, для которых дата начисления недоступна для редактирования.

Для детального анализа отчета P&L можно нажать на ячейку с определенной суммой и посмотреть детализацию расходов или доходов.

Применение отчета P&L для управления бизнесом

Отчет P&L является важным инструментом для анализа финансовой производительности компании и принятия управленческих решений. Он позволяет определить прибыльность бизнеса и проектов, а также прогнозировать экономические результаты.

При использовании отчета P&L в бизнесе можно:

• Определить, какие расходы и доходы составляют основную долю в общей прибыли компании.
• Прогнозировать прибыльность проектов и оценивать их эффективность.
• Анализировать и управлять операционными расходами.
• Оценить рентабельность компании и ее конкурентоспособность.

В итоге, отчет P&L помогает повысить общую прибыльность бизнеса и принимать обоснованные управленческие решения.

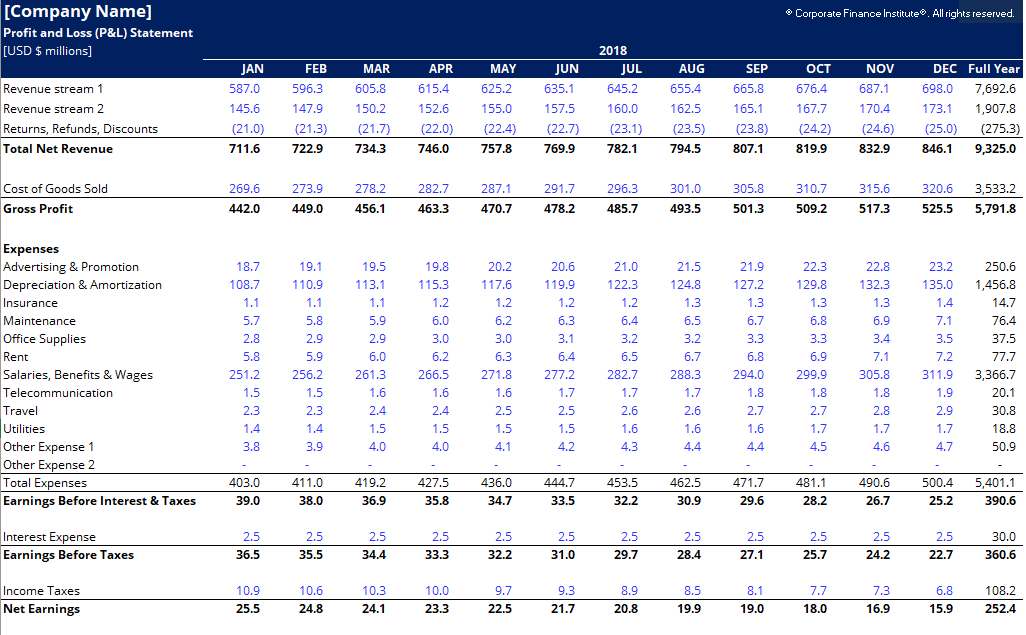
Заключение

Отчет о прибылях и убытках (P&L) является важным инструментом финансового анализа компании. Он позволяет определить прибыльность бизнеса и проектов, а также прогнозировать экономические результаты. Анализ отчета P&L позволяет выявить главные источники доходов и расходов компании, а также эффективно управлять операционными расходами.

Внимательное анализирование отчета P&L и принятие управленческих решений на основе полученных данных помогут повысить прибыльность бизнеса и обеспечить его устойчивое развитие.

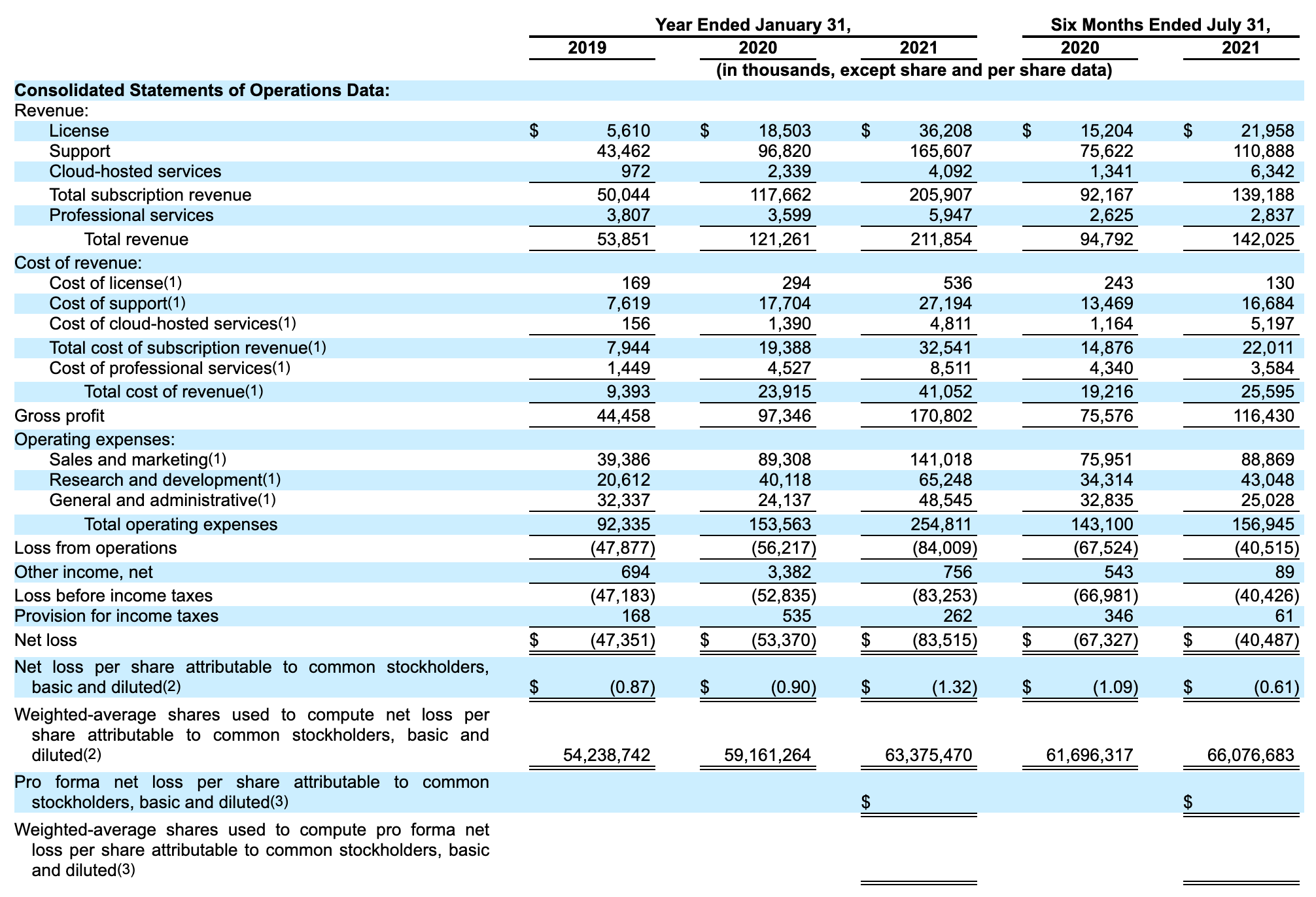
Что нам скажет Википедия?

L_p (также встречается обозначение L_p; читается «эль-пэ»; также — лебеговы пространства) — это пространства измеримых функций, таких, что их p-я степень интегрируема, где p ≥ 1.

L^p — важнейший класс банаховых пространств. L² (читается «эль-два») — классический пример гильбертова пространства.

Для построения пространств L^p используются L_p-пространства. Пространство L_p(X, F, μ) для пространства с мерой (X, F, μ) и 1 ≤ p < ∞ — множество измеримых функций, определённых на этом пространстве, таких что:

• Как следует из элементарных свойств интеграла Лебега и неравенства Минковского, пространство L^p(X, F, μ) линейно.

На линейном пространстве L^p(X, F, μ) вводится полунорма:

• Неотрицательность и однородность следуют напрямую из свойств интеграла Лебега, а неравенство Минковского является неравенством треугольника для этой полунормы.

Далее, на L^p вводится отношение эквивалентности: f ∼ g, если f(x) = g(x) почти всюду. Это отношение разбивает пространство L^p на непересекающиеся классы эквивалентности, причём полунормы любых двух представителей одного и того же класса совпадают. На построенном факторпространстве (то есть семействе классов эквивалентности) L^p/∼ можно ввести норму, равную полунорме любого представителя данного класса. По определению, все аксиомы полунормы сохранятся, и вдобавок в силу изложенного построения оказывается выполненной и положительная определённость.

Факторпространство (L^p/∼, ‖⋅‖_p) с построенной на нём нормой, и называется пространством L^p(X, F, μ) или просто L^p.

Чаще всего данное построение имеют в виду, но не упоминают явно, а элементами L^p называют не классы эквивалентности функций, а сами функции, определённые «с точностью до меры нуль».

При 0 < p < 1 L^p не образуют нормированного пространства, так как не выполняется неравенство треугольника, однако образуют метрические пространства. В этих пространствах нет нетривиальных линейных непрерывных операторов.

Норма на L^p вместе с линейной структурой порождает метрику, а следовательно, на пространствах возможно определить сходимость: последовательность функций {fn}n=1∞ ⊂ L^p называют сходящейся к функции f ∈ L^p, если:

По определению, пространство L^p полно, когда любая фундаментальная последовательность в L^p сходится к элементу этого же пространства. Таким образом L^p — банахово пространство.

В случае p = 2 норма порождается скалярным произведением. Таким образом, вместе с понятием «длины» здесь имеет смысл и понятие «угла», а следовательно и смежные понятия, такие как ортогональность, проекция.

Скалярное произведение на пространстве L² вводится следующим образом:

в случае, если рассматриваемые функции комплекснозначные, или:

если они вещественные. Тогда, очевидно:

то есть норма порождается скалярным произведением. Ввиду полноты любого L^p следует, что L² — гильбертово.

Пространство L^∞ строится из пространства L^∞(X, F, μ) измеримых функций, ограниченных почти всюду, отождествлением между собой функций, различающиеся лишь на множестве меры нуль, и, положив по определению: L^∞ — банахово пространство.

Метрика, порождаемая нормой ‖⋅‖_∞, называется равномерной. Также называется и сходимость, порождённая такой метрикой:

Для пространств (L^p)⋆, сопряжённое к L^p, определяется как пространство функционалов, которые линейны и непрерывны на L^p.