Что такое график

График – это чертёж, на котором наглядно показаны числовые данные при помощи линий и графических элементов. Он может использоваться для визуализации солнечной активности, успеваемости учащихся, роста продаж и плана работ. График также может быть художником, работающим с карандашами, или графиком функции в математике. Узнайте подробнее о графиках в различных контекстах. ПингвинКапитал

Определение графика

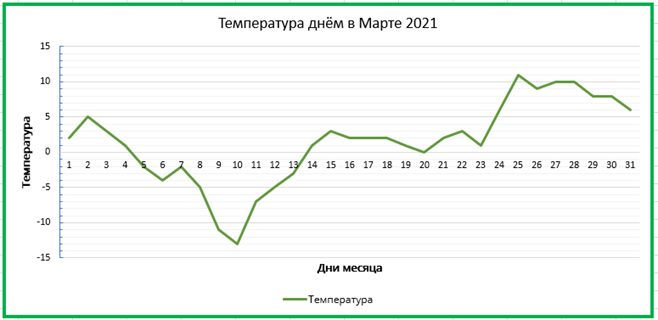
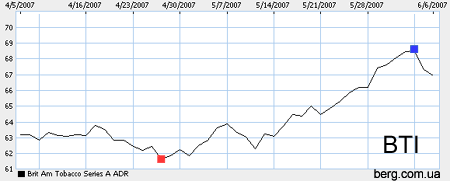
График — это чертёж, на котором наглядно, при помощи линий и других графических элементов показаны какие-либо числовые данные. Это может быть график зависимости солнечной активности от времени, график успеваемости учащихся или график роста продаж.

Также график может быть планом работ, в котором связаны время выполнения проекта и количество производимой продукции. Работать строго по графику означает выполнять задачи в соответствии с установленными сроками. Отставать от графика или опережать график — это отклонения от запланированного выполнения работ.

График работы представляет собой расписание рабочих дней в неделю. Например, у сторожа график работы — сутки через трое.

Определение графика в художественном контексте

В художественной сфере графиком называется художник, который использует в своей работе не краски, а карандаши или другие рисовальные инструменты. Такой художник называется графиком.

График функции в математике

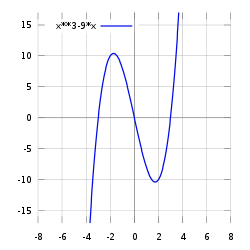
График функции — это геометрическое понятие в математике, которое даёт представление о геометрическом образе функции. Наиболее наглядны графики вещественнозначных функций вещественного переменного одной переменной.

Для непрерывной функции двух переменных z = f(x, y) их графики представляют собой поверхности в трёхмерном пространстве. Эти поверхности могут быть изображены на плоскости в какой-либо изометрической проекции.

Обычно графики функций строят в прямоугольной системе координат, на плоскости эту систему координат называют декартовой системой координат. Также графики для повышения наглядности часто строят в других системах координат, например, в полярной системе координат или других косоугольных системах координат.

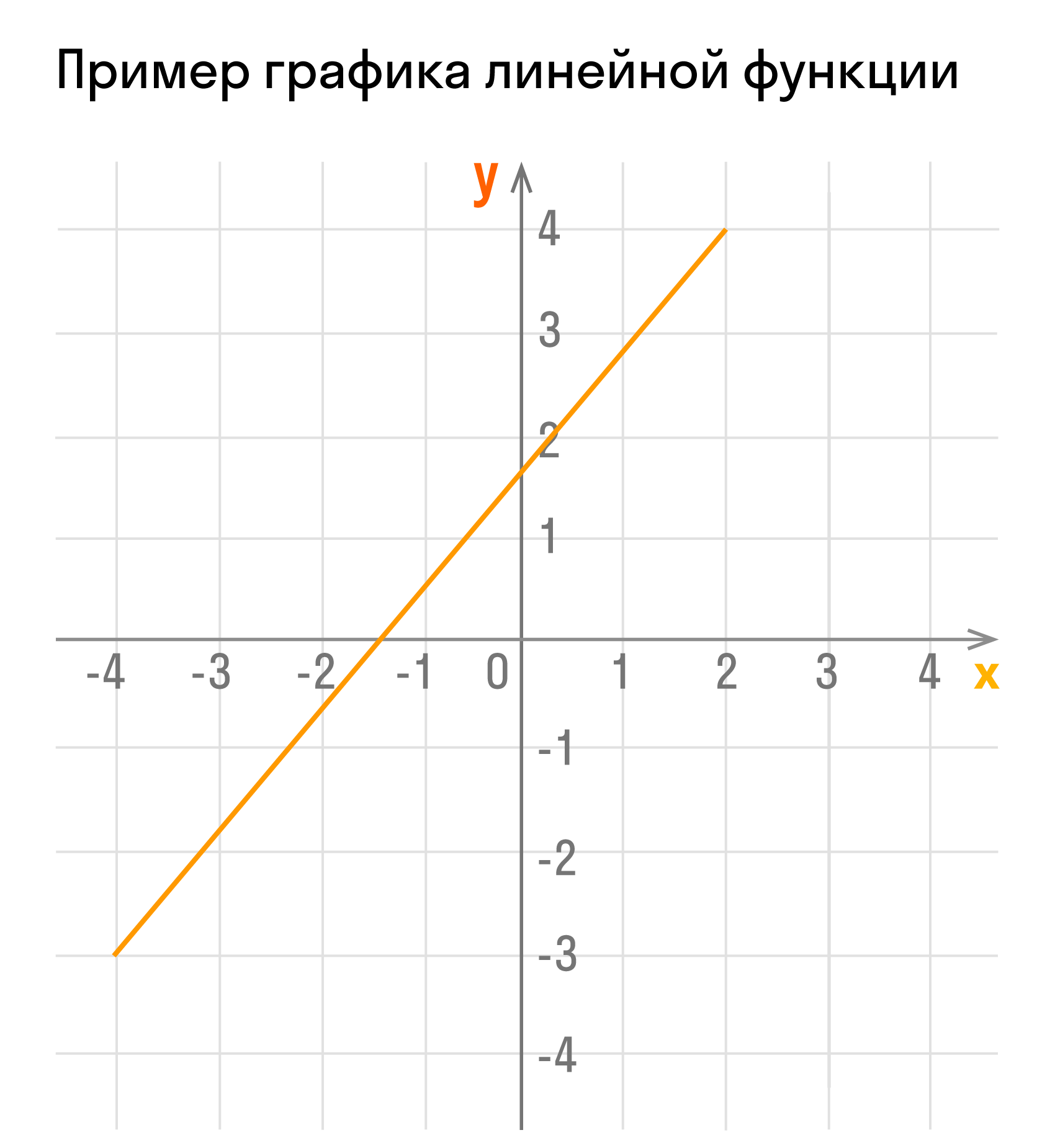
График функции в прямоугольной системе координат представляет собой геометрическое место точек плоскости, абсциссы (x) и ординаты (y) которых связаны отображаемой функцией.

Из определения графика функции следует, что далеко не всякое множество точек плоскости может быть графиком некоторой функции. Например, требование однозначности функции приводит к тому, что никакая прямая, параллельная оси ординат, не может пересекать график функции более чем в одной точке.

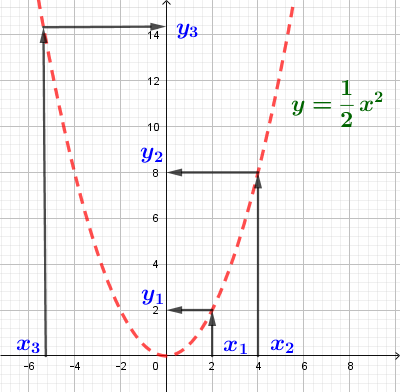
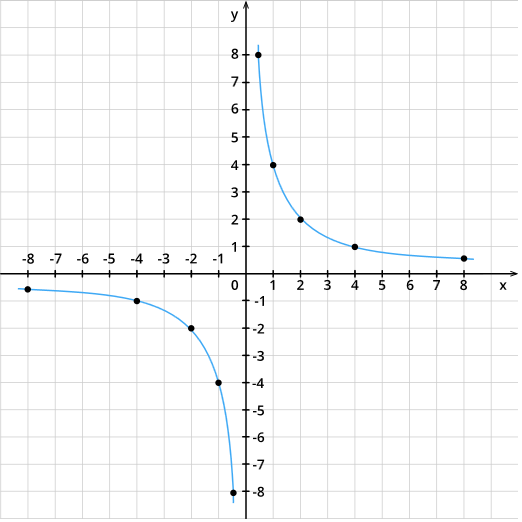
Некоторые функции имеют самостоятельные имена, такие как парабола, гипербола, эллипс и другие.

График в других контекстах

График также может обозначать план выполнения какой-либо последовательности действий с точным указанием сроков и содержания отдельных этапов. Например, график проведения работ или график движения поездов.

Также график может быть расписанием событий или промежутков между событиями по времени. Примером может служить график работы или график движения поездов.

В заключении, график представляет собой графическое изображение данных или план работ, которое позволяет наглядно представить числовую информацию или управлять последовательностью действий. Графики могут использоваться в различных областях, включая науку, экономику, искусство и другие.

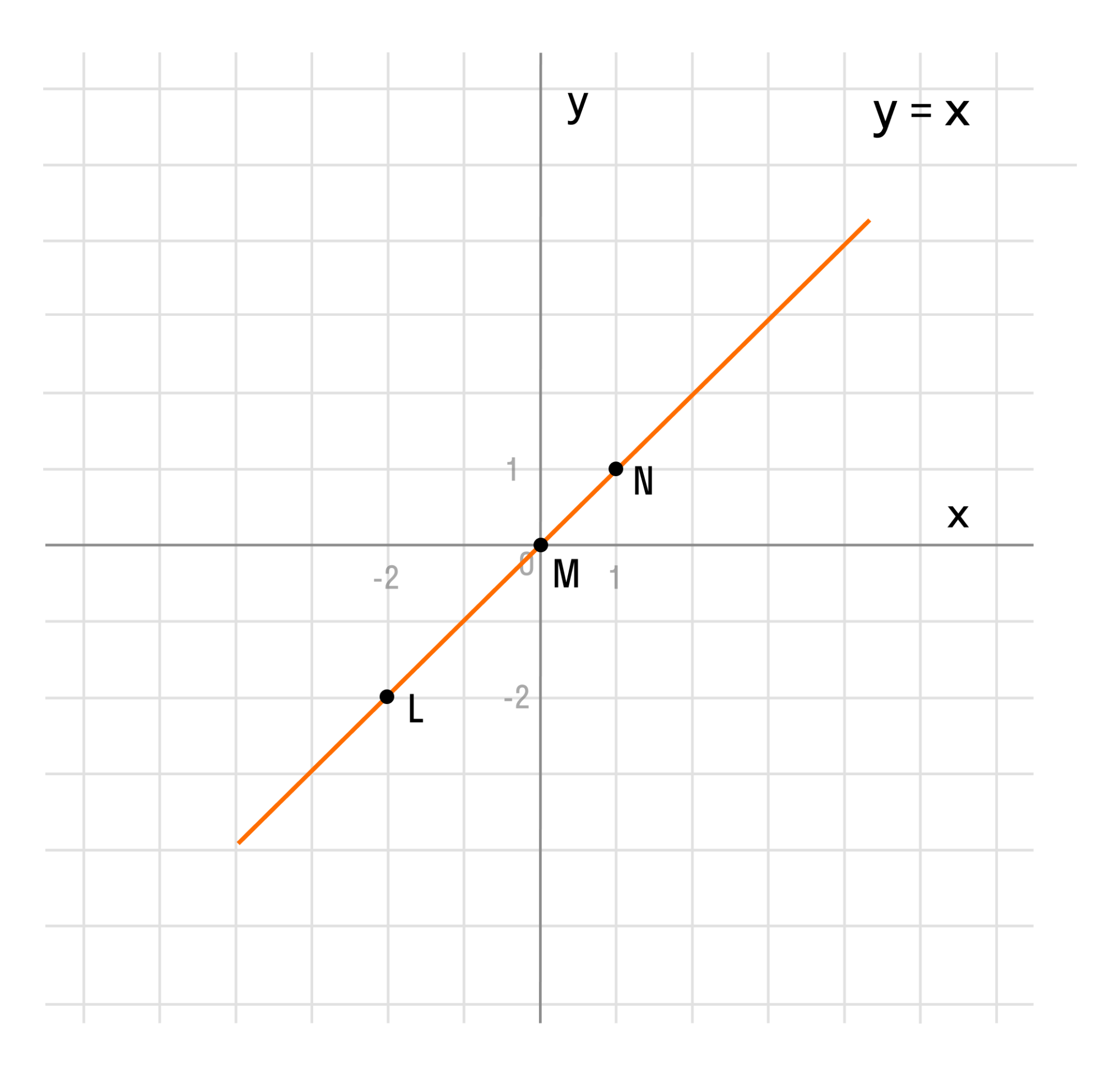
Что нам скажет Википедия?

Гра́фик фу́нкции — геометрическое понятие в математике, дающее представление о геометрическом образе функции.

Наиболее наглядны графики вещественнозначных функций вещественного переменного одной переменной.

Для непрерывной функции двух переменных z = f(x, y) их графики представляют собой поверхности в трёхмерном пространстве, являющиеся геометрическим местом точек z, x, y. Эти поверхности могут быть изображены на плоскости в какой-либо изометрической проекции (см. рисунок).

Обычно графики строят в прямоугольной системе координат, на плоскости эту систему координат называют декартовой системой координат. Также графики для повышения наглядности часто строят в других системах координат, например, в полярной системе координат или других косоугольных системах координат.

В случае использования прямоугольной системы координат, график функции — это геометрическое место точек плоскости, абсциссы (x) и ординаты (y), которые связаны отображаемой функцией:

Таким образом, функция может быть адекватно описана своим графиком.

Из определения графика функции следует, что далеко не всякое множество точек плоскости может быть графиком некоторой функции, например, из требования однозначности функции вытекает, что никакая прямая, параллельная оси ординат не может пересекать график функции более чем в одной точке. Если функция обратима, то график обратной функции (как подмножество плоскости) будет совпадать с графиком самой функции (это, попросту, одно и то же подмножество плоскости).

Некоторые функции определены только в конечном дискретном множестве аргумента, при этом график таких функций представляет собой множество точек, например график функции определённой как:

представляет собой множество из трёх точек (1, a); (2, b); (3, c).

График гладкой (требуемое количество раз дифференцируемой функции) является плоской кривой той же степени гладкости.

Некоторые графики имеют самостоятельные имена, например:

Определение графика:

При рассмотрении отображения произвольного вида f: X → Y, действующего из множества X в множество Y, графиком функции называется следующее множество упорядоченных пар:

В частности, при рассмотрении динамических систем, изображающая точка (t, f(t)) представляет собою график решения соответствующего дифференциального уравнения с заданными начальными условиями такой график часто называют фазовой траекторией системы.